Published on 06 Feb 2021 in Machine Learning

Multi-armed bandits

Introduction

The objective of this lab session is to test the performance of some usual bandit algorithms.

import numpy as np
import matplotlib.pyplot as plt

Algorithms

There are \(k\) possible actions, \(a \in \{ 0, 1,...,k - 1\}\).

We consider the following algorithms:

\(\varepsilon\)-greedy
adaptive greedy
UCB
Thompson sampling

Each algorithm returns an action based on the following inputs:

Variable	Type	Description
`nb_tries`	1D array of int of size `k`	number of tries of each action so far
`cum_rewards`	1D array of float of size `k`	cumulative reward of each action so far
`param`	mixed	parameter of the algorithm

Note: Use the simple_test function to test the behaviour of the algorithms for binary rewards.

def eps_greedy(nb_tries, cum_rewards, param):
    if param == None:
        eps = 0.1
    else:
        eps = float(param)
    k = np.shape(nb_tries)[0]
    if np.sum(nb_tries) == 0 or np.random.random() < eps:
        return np.random.randint(k)
    else:
        index = np.where(nb_tries > 0)[0]
        return index[np.argmax(cum_rewards[index] / nb_tries[index])]

def adaptive_greedy(nb_tries, cum_rewards, param):
    if param == None:
        c = 1.
    else:
        c = float(param)
    k = np.shape(nb_tries)[0]
    t = np.sum(nb_tries)
    if np.sum(nb_tries) == 0 or np.random.random() < c / (c + t):
        return np.random.randint(k)
    else:
        index = np.where(nb_tries > 0)[0]
        return index[np.argmax(cum_rewards[index] / nb_tries[index])]

def ucb(nb_tries, cum_rewards, param):
    if param == None:
        c = 1. 
    else:
        c = float(param)
    if np.sum(nb_tries == 0) > 0:
        index = np.where(nb_tries == 0)[0]
        return np.random.choice(index)
    else:
        t = np.sum(nb_tries)
        upper_bounds = cum_rewards / nb_tries + c * np.sqrt(np.log(t) / nb_tries)
        return np.argmax(upper_bounds)

def thompson(nb_tries, cum_rewards, param):
    k = np.shape(nb_tries)[0]
    if param == "beta":
        # Beta prior
        try:
            samples = np.random.beta(cum_rewards + 1, nb_tries - cum_rewards + 1)
        except:
            samples = np.random.random(k)
    else:
        # Normal prior
        samples = np.random.normal(cum_rewards / (nb_tries + 1), 1. / (nb_tries + 1))
    return np.argmax(samples)

def get_action(algo, nb_tries, cum_rewards, param = None):
    if algo == "eps_greedy":
        return eps_greedy(nb_tries, cum_rewards, param)
    elif algo == "adaptive_greedy":
        return adaptive_greedy(nb_tries, cum_rewards, param)
    elif algo == "ucb":
        return ucb(nb_tries, cum_rewards, param)
    elif algo == "thompson":
        return thompson(nb_tries, cum_rewards, param)

def get_bernoulli_reward(a, model_param):
    return float(np.random.random() < model_param[a])

def simple_test(algo, model_param = [0.1, 0.6, 0.3], time_horizon = 20, param = None):
    k = len(model_param)
    nb_tries = np.zeros(k, int)
    cum_rewards = np.zeros(k, float)
    print ("action -> reward")
    for t in range(time_horizon):
        a = get_action(algo, nb_tries, cum_rewards, param)
        r = get_bernoulli_reward(a, model_param)
        print(str(a) + " -> " + str(int(r)))
        nb_tries[a] += 1
        cum_rewards[a] += r
    index = np.where(nb_tries > 0)[0]
    best_action = index[np.argmax(cum_rewards[index] / nb_tries[index])]
    print("Best action (estimation) = ", best_action)

algos = ["eps_greedy", "adaptive_greedy", "ucb", "thompson"]

algo = algos[3]
simple_test(algo)

action -> reward
-> 0
-> 0
-> 0
-> 1
-> 1
-> 1
-> 1
-> 1
-> 1
-> 1
-> 1
-> 1
-> 0
-> 1
-> 1
-> 1
-> 1
-> 0
-> 0
-> 1
Best action (estimation) =  1

Regret and precision

We now compare the performance of the algorithms in terms of regret and precision.

We consider two models: Bernoulli rewards and normal rewards.

def get_reward(a, model, model_param):
    if model == "bernoulli":
        return float(np.random.random() < model_param[a])
    elif model == "normal":
        return np.random.normal(*model_param[a])

def simulate(model, model_param, time_horizon, algo, param = None):
    k = len(model_param)
    nb_tries = np.zeros(k, int)
    cum_rewards = np.zeros(k, float)
    action_seq = []
    reward_seq = []
    for t in range(time_horizon):
        a = get_action(algo, nb_tries, cum_rewards, param)
        r = get_reward(a, model, model_param)
        nb_tries[a] += 1
        cum_rewards[a] += r
        action_seq.append(a)
        reward_seq.append(r)
    return action_seq, reward_seq

# Bernoulli rewards
model = "bernoulli"
model_param = [0.1, 0.6, 0.3]
time_horizon = 20
algo = algos[1]
action_seq, reward_seq = simulate(model, model_param, time_horizon, algo)
print(action_seq)
print(reward_seq)

[0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
[0.0, 1.0, 1.0, 1.0, 0.0, 1.0, 0.0, 1.0, 1.0, 0.0, 1.0, 1.0, 0.0, 0.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0]

# Normal rewards
model = "normal"
model_param = [(2,1), (2.5,1)]
action_seq, reward_seq = simulate(model, model_param, time_horizon, algo)
print(action_seq)
print(reward_seq)

[0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[1.179115746836822, -1.7287995218220553, 2.9824932372612576, 4.70929759324456, 2.680146152730028, 1.4290308142715937, 1.8901714668658633, 2.400874122036182, 2.343488568046762, 2.945493694373399, 1.5180819830660592, 0.6047846869116558, 2.3886517354112042, 1.121706354860382, 2.2243707175008653, 2.0388350243462257, 2.1270553228483826, 1.3483034375420133, 0.8298318872576476, 1.1361810591475932]

Note: The get_best_action function returns the list of best actions and the corresponding expected reward.

def get_best_action(model, model_param):
    if model == "bernoulli":
        best_reward = np.max(model_param)
        best_actions = list(np.where(model_param == best_reward)[0])
    elif model == "normal":
        means = [model_param[a][0] for a in range(len(model_param))]
        best_reward = np.max(model_param)
        best_actions = list(np.where(means == best_reward)[0])
    return best_actions, best_reward

def get_metrics(action_seq, reward_seq, best_actions, best_reward):
    time_horizon = len(action_seq)
    regret = best_reward * np.arange(time_horizon) - np.cumsum(reward_seq)
    precision = np.cumsum([int(a in best_actions) for a in action_seq]) / (np.arange(time_horizon) + 1)
    return regret, precision

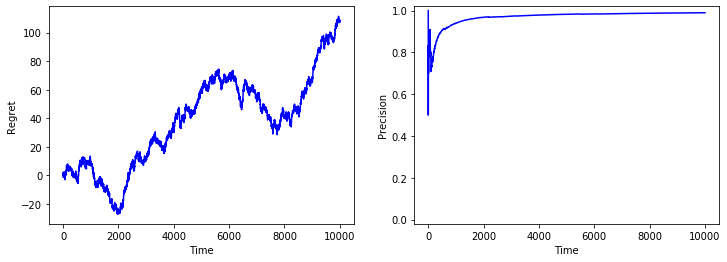
def show_metrics(metrics):
    fig, (ax1, ax2) = plt.subplots(1,2,figsize=(12, 4))
    ax1.set_xlabel('Time')
    ax1.set_ylabel('Regret')
    ax1.plot(range(time_horizon),metrics[0], color = 'b')
    ax2.set_xlabel('Time')
    ax2.set_ylabel('Precision')
    ax2.set_ylim(-0.02,1.02)
    ax2.plot(range(time_horizon),metrics[1], color = 'b')
    plt.show()

time_horizon = 10000
model = "bernoulli"
model_param = [0.2, 0.5]

algo = algos[2]
results = simulate(model, model_param, time_horizon,  algo)
metrics = get_metrics(*results, *get_best_action(model, model_param))
show_metrics(metrics)

png

Statistics

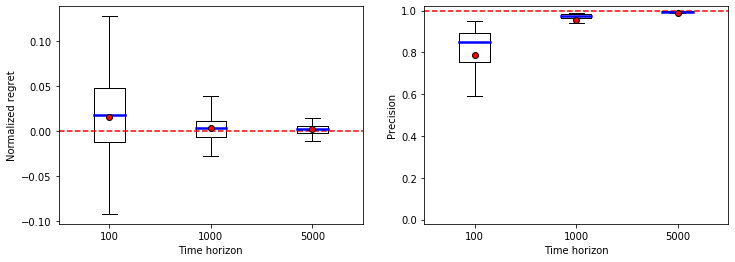
Finally, we provide some statistics on the performance of each algorithm for different time horizons.

def get_stats(nb_samples, time_periods, model, model_param, algo, param = None):
    time_horizon = max(time_periods)
    norm_regret_samples = [[] for t in time_periods]
    precision_samples = [[] for t in time_periods]
    for s in range(nb_samples):
        results = simulate(model, model_param, time_horizon, algo, param)
        regret, precision = get_metrics(*results, *get_best_action(model, model_param))
        for i,t in enumerate(time_periods):
            norm_regret_samples[i].append(regret[t - 1] / t)
            precision_samples[i].append(precision[t - 1])
    return norm_regret_samples, precision_samples

def show_stats(time_periods, stats):
    meanprops = dict(marker='o', markeredgecolor='black', markerfacecolor='r')
    medianprops = dict(linestyle='-', linewidth=2.5, color = 'b')
    fig, (ax1, ax2) = plt.subplots(1,2,figsize=(12, 4))
    ax1.boxplot(stats[0], positions = range(len(time_periods)), showfliers = False, showmeans = True, meanprops = meanprops, medianprops = medianprops)
    ax1.axhline(linestyle = '--', color = 'r')
    ax1.set_xticklabels(time_periods)
    ax1.set_xlabel('Time horizon')
    ax1.set_ylabel('Normalized regret')
    ax2.boxplot(stats[1], positions = range(len(time_periods)), showfliers = False, showmeans = True, meanprops = meanprops, medianprops = medianprops)
    ax2.set_ylim(-0.02,1.02)
    ax2.axhline(y = 1, linestyle = '--', color = 'r')
    ax2.set_xticklabels(time_periods)
    ax2.set_xlabel('Time horizon')
    ax2.set_ylabel('Precision')
    plt.show()

time_periods = [100,1000,5000]
nb_samples = 100
model = "bernoulli"
model_param = [0.1, 0.2]
algo = algos[3]
stats = get_stats(nb_samples, time_periods, model, model_param, algo)

show_stats(time_periods, stats)

png